Functions

Functions#

Exercise 1: Turn this code into a function#

The code below computes the cumulative sum over the values in a list.

Given a list [1,2,3], the cumulative sum is a new list with these items: [1, 1+2, 1+2+3] = [1, 3, 6].

Turn this code into a function with the following properties:

  • name: cumsum

  • argument: a list

  • returns: the cumulative sum

Document this function with an appropriate docstring.

Test your function by making up a new list and calculating the cumulative sum over its values.

values = [1,2,3,4,3,2,4]

cumsum = []
for idx in range(len(values)):
    cumsum.append(sum(values[:idx+1]))

print(cumsum)

# your solution here

[1, 3, 6, 10, 13, 15, 19]
[1, 3, 6, 10, 13, 15, 19]

[1, 0, -2]

Exercise 2: Use a python function to calculate the values of a mathematical function#

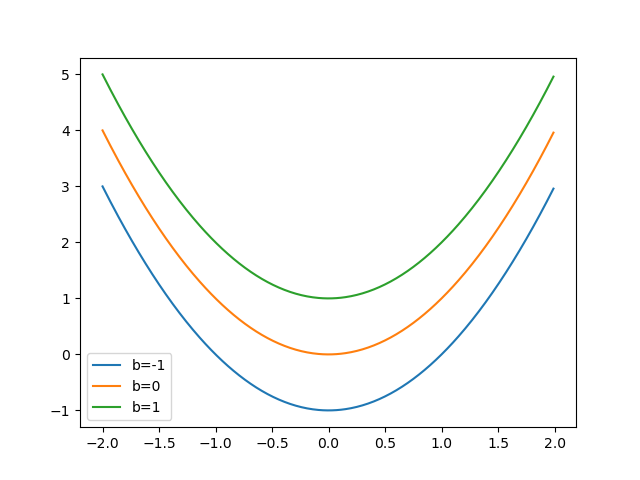
Write a function that computes the value of the following mathematical function: \(f(x,b) = x^2 + b\)

Plot the function \(f\) for 100 x-values covering the range of [-2.0, 2.0] and three different, but constant, values of b = [-1, 0, 1]. This should produce three curves, each with 100 data points.

Annotate the plot with proper labels and a legend that indicates the vale of b.

Roughly like so:

# your solution here

Exercises 3: Organizing code with functions#

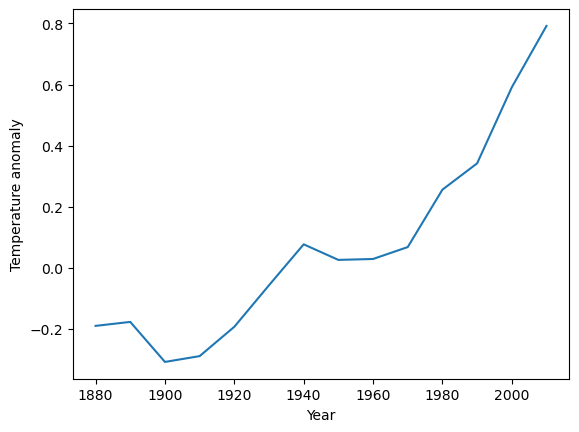
For the next block of exercises, we will play with temperature anomaly data - deviations of the global mean temperature. We will first solve the problem without using functions (Exercise 3) and then improve the solution by using functions (Exercise 4).

# EXECUTE BUT DO NOT CHANGE THIS CELL
temperature_anomalies = [-0.19,-0.177,-0.308,-0.289,-0.193,-0.057,0.077,0.026,0.029,0.068,0.256, 0.342, 0.591, 0.792]
print(temperature_anomalies)

[-0.19, -0.177, -0.308, -0.289, -0.193, -0.057, 0.077, 0.026, 0.029, 0.068, 0.256, 0.342, 0.591, 0.792]

For an analysis, we need to z-score the data:

Z-scoring is a common operation in statistics. It involves normalizing the data so that it has zero mean and unit standard deviation (std=1).

This can be done by applying the following two steps to each value in the list:

  1. subtract the mean,

  2. divide by the standard deviation:

In math: \(z = (x - M) / S\) where \(z\) is the z-scored value and \(M\) and \(S\) are mean and standard deviation of the data.

In the followign 4 exercises, we will show you how to approach such a problem using the divide and conquer strategy: We split the big, complicated, seemingly unsolvable problem into simpler sub-problems, that are easy to solve. Each exercise that follows solves on such subproblem.

We will:

  1. Compute the sum over all elements in a list

  2. Compute the mean, by modifying the code from step 1.

  3. Generate a list in which the mean was substracted from each list element

  4. Compute the standard deviation

  5. Generate a list in which each list element is z-scored (mean subtraced, divided by the standard deviation)

Exercise 3.1 - Compute the sum of all anomaly values#

The sum of all list values can be written in sum notation as follows:

\(A = \sum_i^N x_i\)

where:

  • \(A\) is the sum

  • \(N\) is the number of elements in the list

  • \(x_i\) is the i-th element in the list, i can range from 0 to N-1

# your solution here

Exercise 3.2 - Compute the mean of all anomaly values#

The mean is defined as the sum of all values, \(A\), divided by the number of values in the list, \(N\):

\(M = A/N = 1/N \sum_i^N x_i\)

# your solution here

Exercise 3.3 - substract the mean value#

Create a new list, mean_subtracted that holds the mean-subtracted anomaly values. Subtract the mean of the anomaly values from each element in temperature_anomalies such that \(y_i = x_i - M\).

# your solution here

Exercise 3.4 - Compute the standard deviation#

The standard deviation can be computed by:

  1. subtracting the mean from each element of the list

  2. taking the square of each mean-subtracted value

  3. calculating the mean of the squared, mean-subtracted values (this is the variance)

  4. taking the square root of the variance

Or more cryptically:

\(S = \sqrt{1/N \sum_i^N (x_i - M)^2} = \sqrt{1/N \sum_i^N y_i^2}\)

# your solution here

Exercise 3.5 - z-score#

Now create a new list of z-scored anomaly values by re-using the values for mean and standard deviation computed above and applying them to each value in the list:

\(z_i = (x_i - M) / S\)

# your solution here

Exercise 4: Re-organize the code from exercise 3 using functions#

Write four functions:

  1. One that computes the sum of the elements of a list.

  2. One that computes the mean of the elements of a list. Use your sum created in step 1.

  3. One that subtracts a specific value from all elements in a list.

  4. One that computes the standard deviation of the elements of a list. Use the mean function computed in step 2.

  5. One that zscores the list elements (returns a new list in which each element is z-scored). Re-use the functions created in the previous steps.

In each step, first think about the inputs (arguments) and outputs (return) of each function.

# EXECUTE BUT DO NOT CHANGE THIS CELL
temperature_anomalies = [-0.19,-0.177,-0.308,-0.289,-0.193,-0.057,0.077,0.026,0.029,0.068,0.256, 0.342, 0.591, 0.792]
print(temperature_anomalies)

[-0.19, -0.177, -0.308, -0.289, -0.193, -0.057, 0.077, 0.026, 0.029, 0.068, 0.256, 0.342, 0.591, 0.792]

4.1 Write a function that calculates the sum of all list elements#

# your solution here

4.2 Function for calculating the mean#

# your solution here

4.3. Function for subtracting the mean#

# your solution here

4.4 Function for calculating the standard deviation#

# your solution here

4.5 Function for z-score a list#

# your solution here
Contents